Integer Graphics: Line Intersection
Graphics can be a tricky topic, particularly when attempting to find anything on the internet these
days that provides solution in terms of integer-only maths.
embedded-graphics is a (mostly) integer-only library,
so in pursuing a solution to good line joints for the Polyline and Polygon shape
implementations, a bit of interweb detective work was required.
I eventually stumbled upon this StackOverflow question, the answers to which mostly seem to do what I'm looking for. I'm not a good mathematician by any means so the below code might not be stable in all situations, but it seems to work in a quick demo I whipped up.
I also posted the solution here on StackOverflow for posterity.
/// 2D integer point
/// Line primitive
/// Check signs of two signed numbers
///
/// Fastest ASM output compared to other methods. See: https://godbolt.org/z/zVx9cD
/// Integer-only line segment intersection
///
/// If the point lies on both line segments, the second tuple argument will return `true`.
///
/// Inspired from https://stackoverflow.com/a/61485959/383609, which links to
/// https://webdocs.cs.ualberta.ca/~graphics/books/GraphicsGems/gemsii/xlines.c
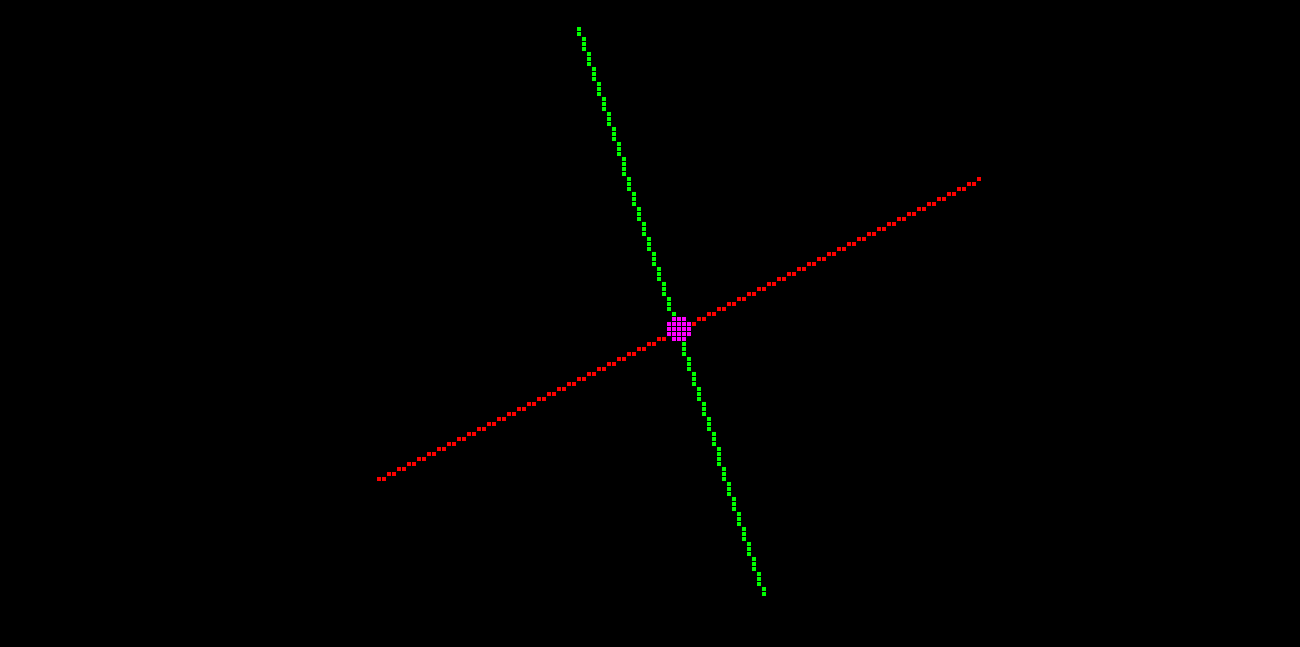
In the demo, two line segments (red and green) are drawn. If they intersect and the point of intersection is on both line segments, a magenta dot is drawn at that point:
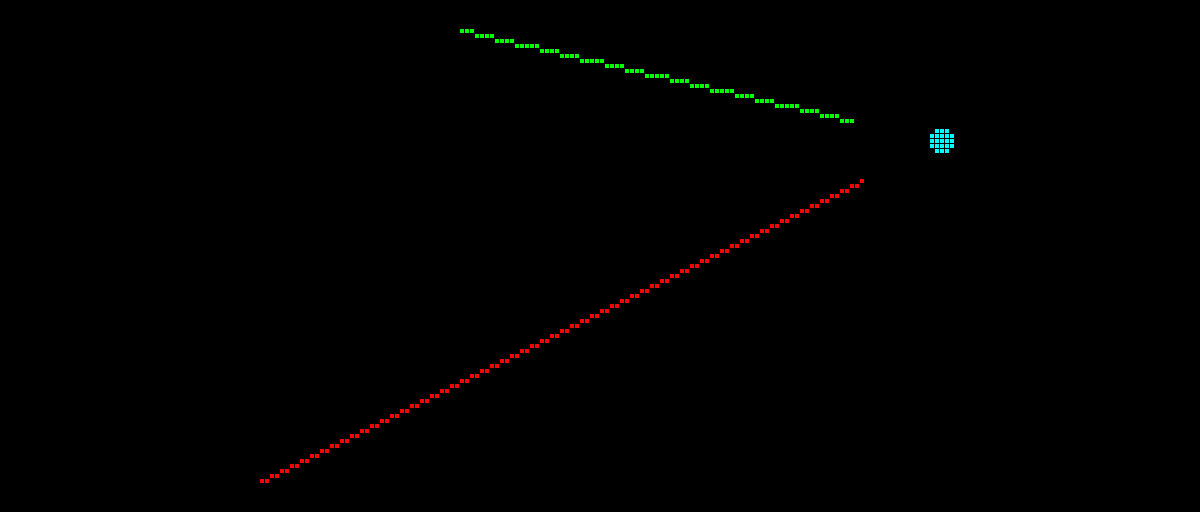
If the lines intersect, but the intersection does not lie on both line segments (i.e. the
is_on_segments flag is false) , a cyan dot is drawn at the intersection:
 .
.
Now that this is out of the way, I should be able to focus on getting thick line support for polylines, polygons and triangles working, as the above intersection logic is required to get "miter" style joints working correctly.
