Optimising Rust: Clockwise Triangles
Welcome to another pointless tangent into the exciting world of line joints in
embedded-graphics! embedded-graphics is an integer
only, iterator based no-std graphics library for environments with low resource availability. This
time, we'll be looking at some not-so-great optimisations made to a point sorting function.
Update: A kind Twitter user pointed out a more optimised solution for triangles which you can find here.
Some context
I've already covered integer-only line intersections, a building block for computing the corners of both mitered and bevelled line joints. Between then and now, I've written some test code to triangulate between these computed corners and form a set of thick lines. Below is an example of a triangle. You can see (if you squint hard enough) the wireframe component triangles on the left, and the final filled triangle on the right. Looks alright!
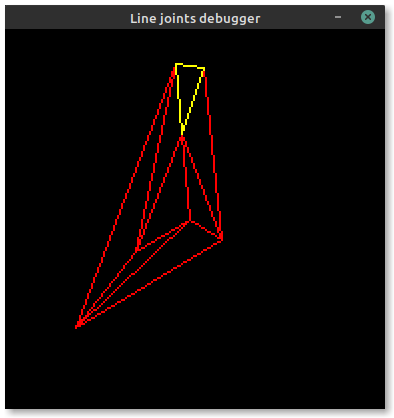
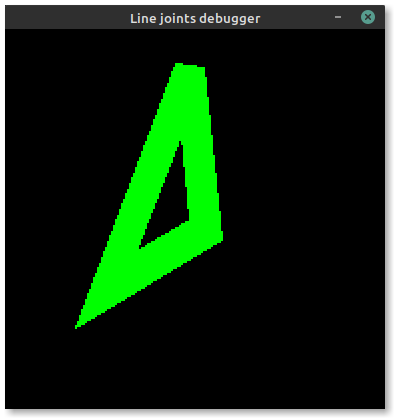
Now the issue is stroke offsets. Embedded-graphics allows three stroke positions relative to the theoretical "skeleton" lines of a shape: centered, inside and outside. To ensure the offset remains on the same side of each edge of the triangle (or polygon), we need to ensure that all points in the shape are sorted in clockwise order. This allows us to derive the outside lines highlighted in magenta in the image below:
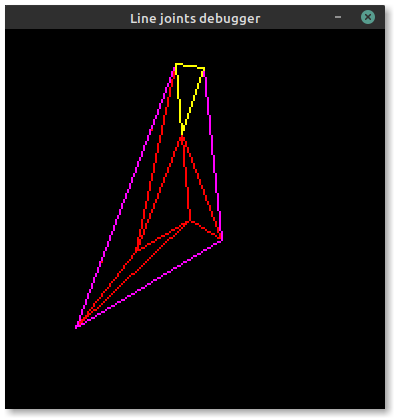
If the points aren't sorted correctly, some lines will flip sides over their length.
The approach
I'll focus on triangles for this article, but the approach described here should work for any number of points.
Because embedded-graphics aims to be as fast as possible, it tries to avoid floating point maths
when possible. Conventional triangle sorting algorithms use the dot product of two vectors to
determine order, which typically requires a tan() call (I think? What do I look like, a
mathsologist?) so we'll have to find a different solution.
Luckily, there's an integer-only method as described in this Stackoverflow answer to sort two points by angle.
We can use this sorting function as a predicate to the builtin sort_unstable_by method in Rust,
but we need to make a few changes first.
This is the original C(++?) from https://stackoverflow.com/a/6989383/383609:
bool
This needs porting to performant Rust, so let's crack on.
More junk
First, though, we need some supporting code.
Let's say we define a Triangle with three Points like this:
Where Point is:
We need a way to create triangles, and a way to get a triangle with all of its points sorted in clockwise order. Thus:
Notice the sort_clockwise function buried in there? That's what we'll focus on.
Note: I'm getting the triangle's bounding box and using its center instead of finding the true triangle "center of gravity" here - it's fast, and good enough for the purposes I need this method for.
Straight port from C/C++ to Rust
This is a syntax port of the original code to Rust. Pretty straightforward.
There's not much to mention here other than the fact we're still returning a bool. This needs to
be wrapped in a match to be usable by sort_unstable_by in Triangle::sorted_clockwise:
points.sort_unstable_by;
Changing to use Ordering
The above code doesn't feel very Rust-like, but we'll try and fix that better in a bit. For now
though, one good cleanup to make is to stop returning a bool and return an Ordering directly:
That's better! In terms of style, I'm happy with where this is at so I won't change it any futher. Performance-wise, though, surely we can tune it some more?
Performance tuning
First, one of the simplest optimisations is present in the original code: don't do work you don't
have to! For example, the det variable is only computed if the function falls through to where
it's needed.
Next are some attempts I made at optimising this code a bit better.
Hoist some comparisons
Recomputing the same thing a few times seems pointless, so I'll hoist the two negations into the
variables d_ax and d_bx for reuse.
Use .cmp and Ordering tricks
We've hoisted some calculations, but we can also hoist some of the comparisons into cmp_ax and
cmp_bx. This also lets us squash everything into one giant match block. I'm not sure if it's
easier to read, but it sure is some juicy Pro Rust™.
Benchmarking
All benchmarks are run on x64 Linux Mint 20, Ryzen 7 3700X overclocked to 3.8 GHz, 32GB DDR4 3200. I'm using the venerable criterion crate to run the benchmarks and avoid some of the pitfalls when micro-benchmarking.
| Suite | Result (avg) |
|---|---|
| Straight C port (baseline) | 9.4473 ns |
Use Ordering instead of bool | 10.712 ns |
| Hoist some repeated comparisons | 10.160 ns |
Convert everything to a big, single match | 12.024 ns |
Curiously, on x64 at least, all of the nice changes resulted in regressions! Thankfully they're pretty minor, but it was surprising to see that nothing changed for the better. There's a lot of rhetoric in Rust optimisation articles about idiomatic code allowing for better optimisations, but it doesn't seem to apply in this case.
I don't show it here because it'd make the article too long, but I benchmarked a few other triangles with different properties, and all are sorted at pretty much the same speed.
If you're interested, here's the bench code:
use Ordering;
use *;
use ;
criterion_group!;
criterion_main!;
Polygons
What's the performance like for shapes with more than three points (i.e. polygons)? That's easy enough to test with a benchmark with more points in it:
b.iter
A triangle sorts in about about 4ns per point, however the sort doesn't scale linearly. The above benchmark with 14 points sorts in about 140ns, or roughly 10ns per point. This will be overhead in the sorting algorithm, as the sort function itself has a fixed input size.
Final result
Now triangle points are correctly ordered!
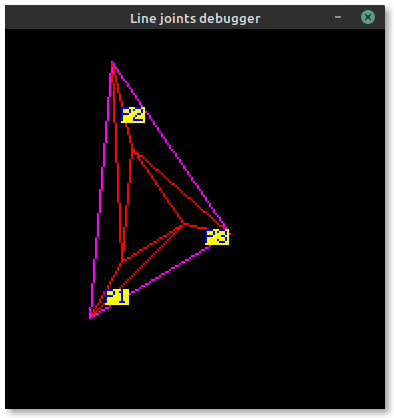
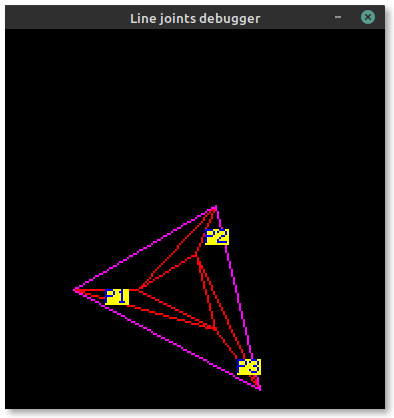
Notice the order of P1, P2 and P3 changes to keep the outside edge on the left of each line.
The only point that is moved between the two screenshots is P2 in the first (becoming P3).
Conclusion
So, which version is best? Considering they all have about the same performance, I went with
sort_clockwise_use_ordering. I think it offers a good balance between readability and performance
(by being basically the same as the naive bool C port). If the other methods improved performance
a large amount, I might've gone with the Pro Rust™ nested match with guards, but it's certainly
not easily read.

Performance stuff is always worth checking if you're not sure! It's also pretty simple with
criterion doing most of the heavy lifting.
That said, always take microbenchmarks with a grain of salt. In this case, that is even more relevant as architecture differences between the target ARMv7 CPUs embedded-graphics is designed for and the beefy x64 the benchmarks are running on may have vastly different performance profiles. Ideally, benchmark on your target hardware if you can.
The final benchmark iteration time is about 10ns on my desktop. This post only discusses part of the final algorithm, so it does add up, but for now there are bigger fish to fry...
Another thing to do would be to look at the generated assembly. This might be important for optimising on ARM targets without being able to run benches on the target hardware, but I'll uhh leave that as an exercise for the reader because I can barely read assembly as it is, let alone grok the performance of individual instructions.
If you got this far, thanks for reading! If you need a fast, featureful, flexible, easy to use graphics library for your no-std environment, consider using
embedded-graphicsfor your next project. It even comes with a simulator!.If you found this article or
embedded-graphicsitself useful, please consider supporting my work on Github sponsors or Liberapay.

